Power Query or the Power BI Get Data Experience uses a functional language called M to perform its Data Preparation or Data Transformation processes.
You can read this article to get to know more about Power Query and the M language, but in short, Power Query is the interface that assists you, through buttons and dialogs, to create the M code for you.
Now, where would I see a function, an argument or a parameter in Power Query ?…and what are they? Let’s have a quick example to see them in real life.
Imagine that we have a table like the following:
[table style=”solid”]
| Header |
|---|
| 1 |
| 2 |
| 3 |
[/table]
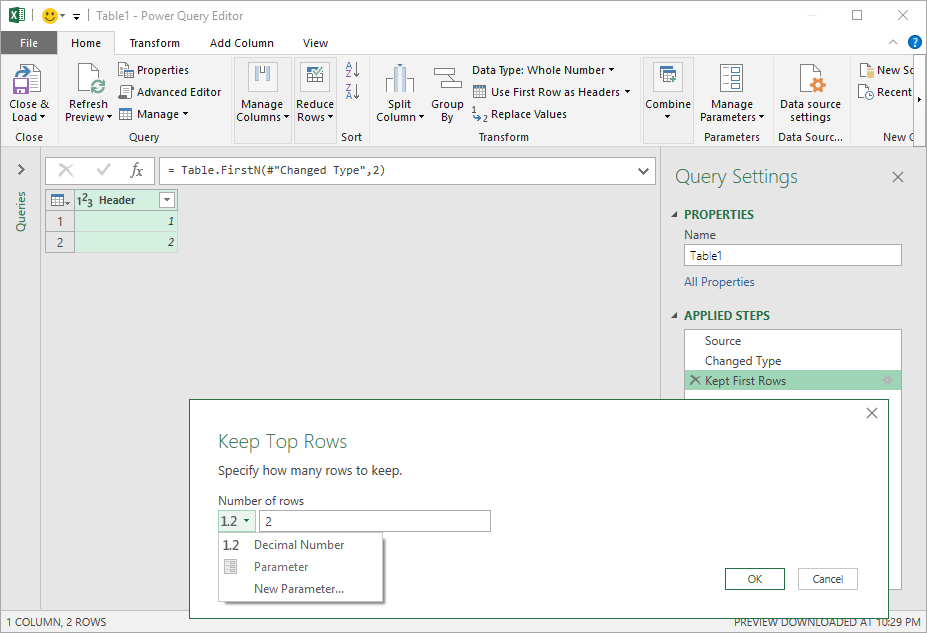
Now let’s go ahead and load that to Power Query and simply do a Keep Rows –> Keep Top Rows
You’ll notice that we get a new window called Keep Top Rows where we can input the value for the number of rows that we want to keep.
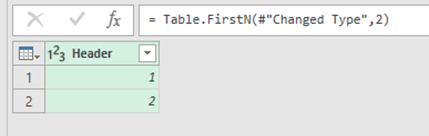
Check what the formula bar says:
By clicking that Keep Top Rows button, Power Query has automatically created a new step and used the correct function for us.
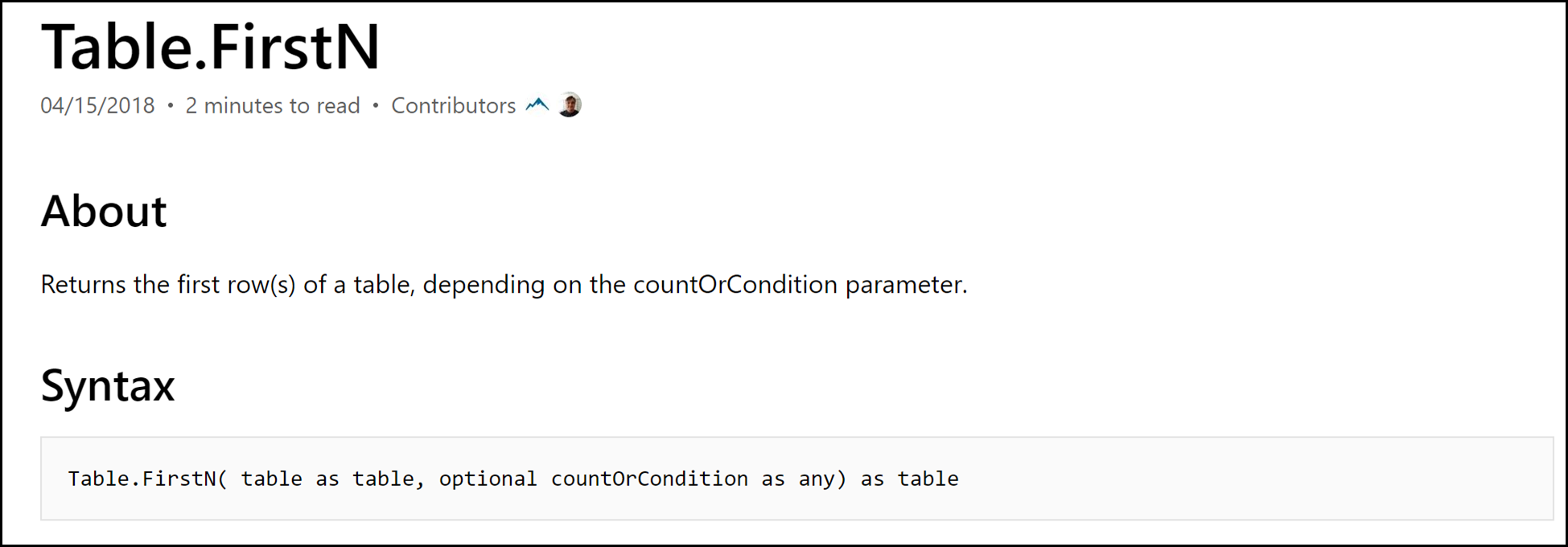
It is using a function called the Table.FirstN which takes 2 parameters.
Function parameters are the names listed in the function definition
You can read the full documentation of the Table.FirstN function here. The function parameters are:
- Table – the table to check
- optional countOrCondition – Depending on the type, more than one row will be returned.
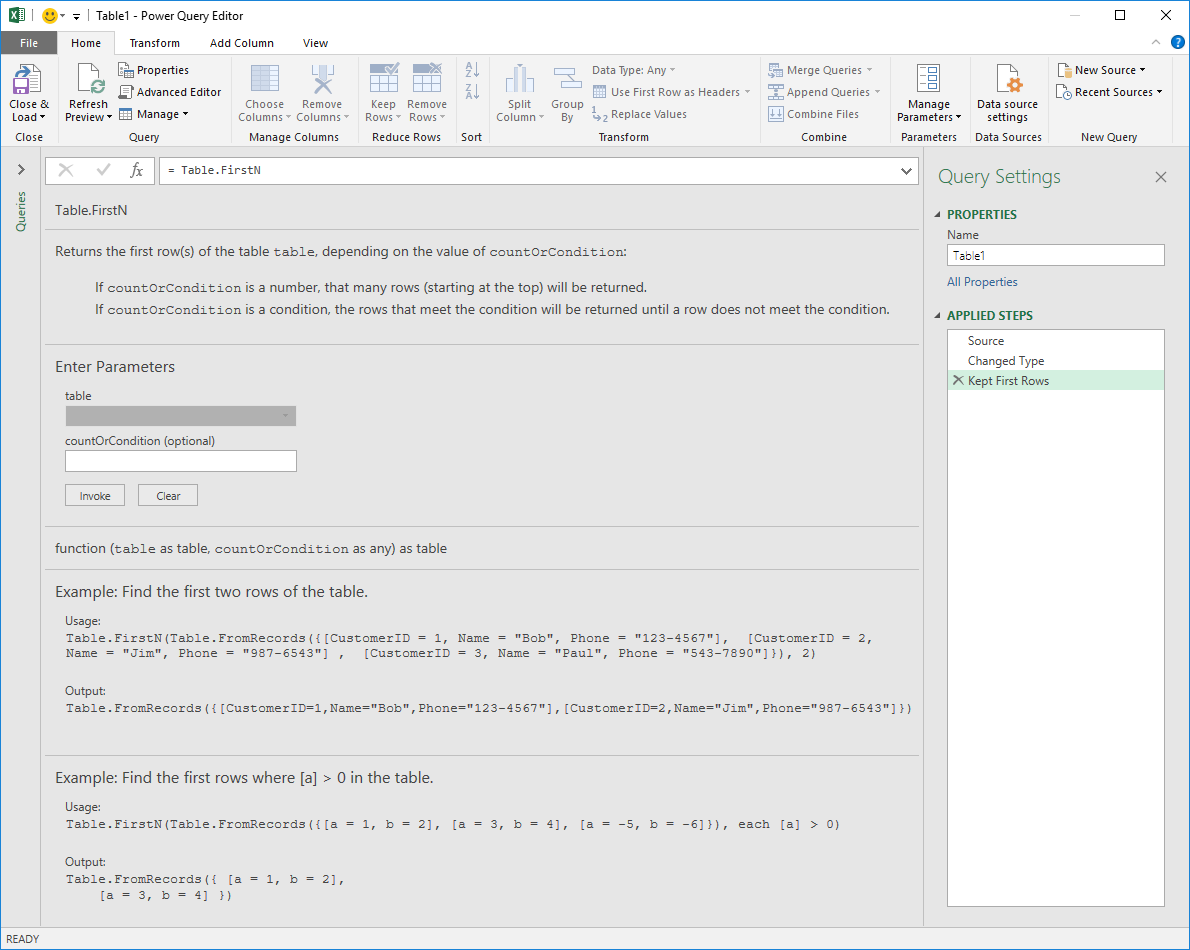
Another way to get the full documentation of a function is to simply type it in the formula bar and hit enter:
Function arguments are the real values passed to (and received by) the function
Going back to what we see in the formula bar and the formula that was created for us, we notice that some arguments were passed to the function:
We know that the first parameter of the function requires a table and we see the name of our previous step, which is a table, passed to this parameter as the first argument.
The second parameter requires a count or a condition, and in our case we simply used the number 2, so we want the top 2 rows from this table.
This number 2 is our second argument.
User defined Parameters / Variables
In the pictures where you see the Keep Top Rows window you’ll notice that there’s a drop-down and inside that drop-down there’s an option for a Parameter.
See, back in 2016, the Power Query team implemented a way for users to define their own parameters that could be passed to any function/s of their choice.
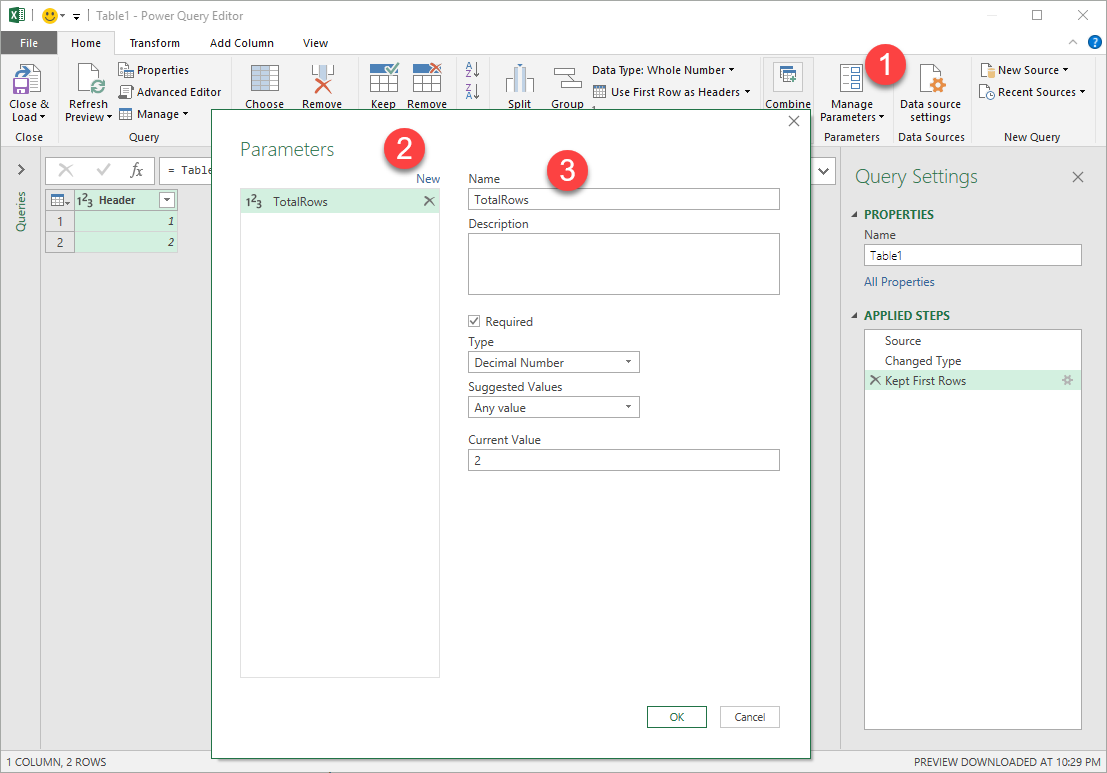
in order to define your own parameter in Power Query / Power BI, you need to follow the following steps:
- Click on the Manage Parameters button
- Now that the Parameters window is loaded, click on Add New Parameter
- Define the Parameter as shown in the image above
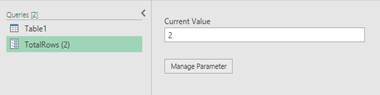
Once you hit OK, you’ll notice that the result will look like this:
and you can now use that Parameter wherever you want, but it is more commonly passed as an argument to functions.
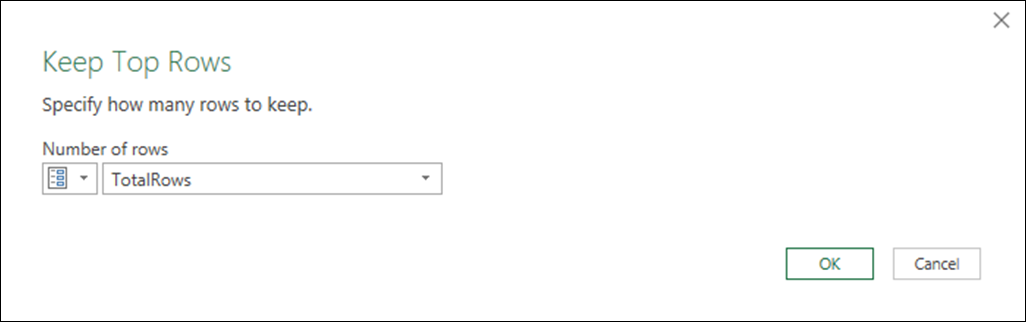
Let’s do a quick example with our previous query where we can simply replace the 2 with the parameter:
You can read more about how to re-configure a step in Power BI / Power Query from this blog post.
The main benefit of Parameters in Power BI / Power Query
There are multiple benefits of Parameters in Power BI / Power Query, but the main point is how you’re essentially creating a parameter and how you change its argument (value) so easily.
Of course, a Parameter can even help you create a User Defined Function and that’s something that we’ll see in the next blog post in this series, but at the very least you can have an easy way to change the argument of your parameter as described in this blog post and showcased in the following video:
Summary and next steps
- A function is a mapping from a set of input values to a single output value. A function is written by first naming the function parameters, and then providing an expression to compute the result of the function.
- Function parameters are the names listed in the function definition
- Function arguments are the real values passed to (and received by) the function
You need to have these concepts clear before into a creating your own function or trying to read and edit M code. These are the core elements of the M language.
In the next posts in this series I’ll go over:
- User Defined Functions in Power Query / Power BI
- Parameter Tables
Got any suggestions or feedback for future blog posts? leave them in the comments section down below.

 Miguel Escobar Published February 12, 2019
Miguel Escobar Published February 12, 2019 








Great post. It might be worth clarifying in your post when you say that:
“A function is a mapping from a set of input values
to a single output value”
…that the value returned could be a primitive value (e.g. number, logical, text, null), a list, a table, or a record.
glad to see you here, Jeffrey!
I tried to keep it super simple since the term value refers to pretty much any value inside of the M language (structured or primitive). Often the feedback that I received is that I get too in depth or too technical with the terms so I’m trying to use the KISS principle 🙂
Yeah I hear you. But of course, a reader might not know what ‘value’ means in context of the conversation, and interpret it in the simplest way…as ‘number’ or ‘text.
Case in point: When I first read your line that “a function is a mapping […] to a single output value” I was scratching my head, thinking “But wait a minute: I thought a function could return a *Table* too, not just a single value”. Which then led me to go look at the definition of ‘value’ in the PQ documentation for the first time, where I learned that ‘value’ didn’t mean what I *thought* it meant.
I realize you’re damned if you do, and damned if you don’t, when it comes to feedback from readers about ‘too technical’ vs ‘not technical enough’ . But in this case, I’m betting that lots of people will misinterpret what ‘value’ means, and then miss something important.
Great post Miguel – in that sense, are parameters similar to variables? For instance, i could use dates as a parameter?
hey Christopher!
I try to not use the word variables because it might create confusion with the term variables in DAX, but from a programming perspective they could be categorized as variables. Therefore, you could have query called “dates” that can be defined as a variable / parameter and the values inside that query would be the arguments that you’d pass to a function.
Perfect – thanks!
Dear Miguel
I am taking the advanced courses from Power Query Academy and have found this article more informative than the course handouts. This applies to other advanced topics too and I am using your blogs to supplement my learning. Perhaps you and Ken could consider adding a bit more material to the course handouts.
Thanks.
Thanks for your comment, Raymond!
You can think of this blog as a diary of sorts where I try to expose my ideas and understandings. In some cases they are not the most ideal explanations or haven’t received enough feedback, and that’s the main reason why we are a bit hesitant to add it directly to the academy before putting it through a QA phase.
I’m happy to know that you find it valuable!
I will run this by Ken and see what he has to say. Hope you enjoy the rest of the posts as well!
hi
i define stored procedure in sql with 2 parameter
and in power bi descktop define 2 paramter and i used them as store procedure paramterer
now in power bi desktop i can change paramteres value
but i want my end user in power bi report servrer can change paramtere value ,too
is there any solution?
such as use text box or ang thing that end user can enter value and i transfer it to store procedure
Hey!
Not sure if You can do it in Report Server, but in the “data source” settings inside the power BI service there’s a section called “parameters” where you can change the parameters used in your queries:
https://docs.microsoft.com/en-us/power-bi/connect-data/service-parameters
Perhaps you’ll be better off with a different approach rather than using stored procedures. Tough to say, but it’s usually easier to create a model where the user can leverage simple slicers or filters without having to query the data source in the service unless you need real time analytics in which case you can use direct query